潮气量的另一个视角:从统计数据到不确定性
时间:2024-07-15 16:02:36 热度:37.1℃ 作者:网络

我们饶有兴趣地阅读了 Pellegrini 等人最近发表的社论。毫无疑问,我们现在比以往任何时候都更开始质疑潮气量(VT)在急性呼吸窘迫综合征(ARDS)中的真正作用。正如前文所述,有两个问题仍未得到解答,我们认为这些问题比想象的还要复杂,应该从不同的角度来探讨。
1.驱动压(ΔP)是否是不安全 VT 的指标,是否对结果有直接影响?从统计学的角度来看,VT 是一个连续变量,具有无限的取值范围。当此类变量被二分法(二元变量)(6 毫升与 10 毫升预测体重)时,统计信息就会丢失(统计熵增加)。换句话说,在估算由基本连续变量导出的二进制变量的平均值时,大多数情况下连续变量的信息不会被利用,而只是使用导出的二进制变量进行估算。这种结果会产生相当大的变异性,而这种变异性与样本量成反比。为了解决这一问题,Li 等人提出了一些通过密度估计的方法。
2.哪些因素会影响呼吸系统的顺应性以及 VT 和 ΔP 之间的相互作用?首先,我们必须将肺视为由弹簧(弹性模块)和阻尼器(粘性模块)并联形成的粘弹性流体(Kelvin-Voigt 体);其次,肺不是一个孤立的系统,必须考虑其容器(肋骨)的不同机械特性。流体和所有物质一样,由分子组成,分子之间有空隙隔开。然而,在数学上确定流体的特性(如密度)时,需要将其概念化为一个连续的场(分子之间没有空隙)。因此,取样体积会变小(微观尺度),否则,为了描述流体的特性,就必须逐个分子(逐个肺泡)进行研究;这就是所谓的 "连续介质假说"(图 1)。在机械通气过程中,会产生不同的模式,从通气良好的肺泡,到有塌陷趋势的肺泡,甚至是同时过度扩张的肺泡,无论肺部状况如何,是全身麻醉下的健康肺还是 ARDS 患者。监测机械通气(MV)的目的是通过实现适当的压力和应变目标,将呼吸机诱发肺损伤的风险降至最低。这一假设有助于我们理解不同监测方案的复杂性。ΔP可视为肺部成分(肺泡顺应性)"微观不确定性 "与肺外成分(胸廓)"宏观不确定性 "之间的关系,以中间尺度表示,为整个肺部提供可通用的信息,以帮助决策。
总之,我们必须明白,仍有许多问题有待解答。因此,我们需要从不同的角度来看待这个问题,以期提出新的假设,帮助我们继续增进知识。
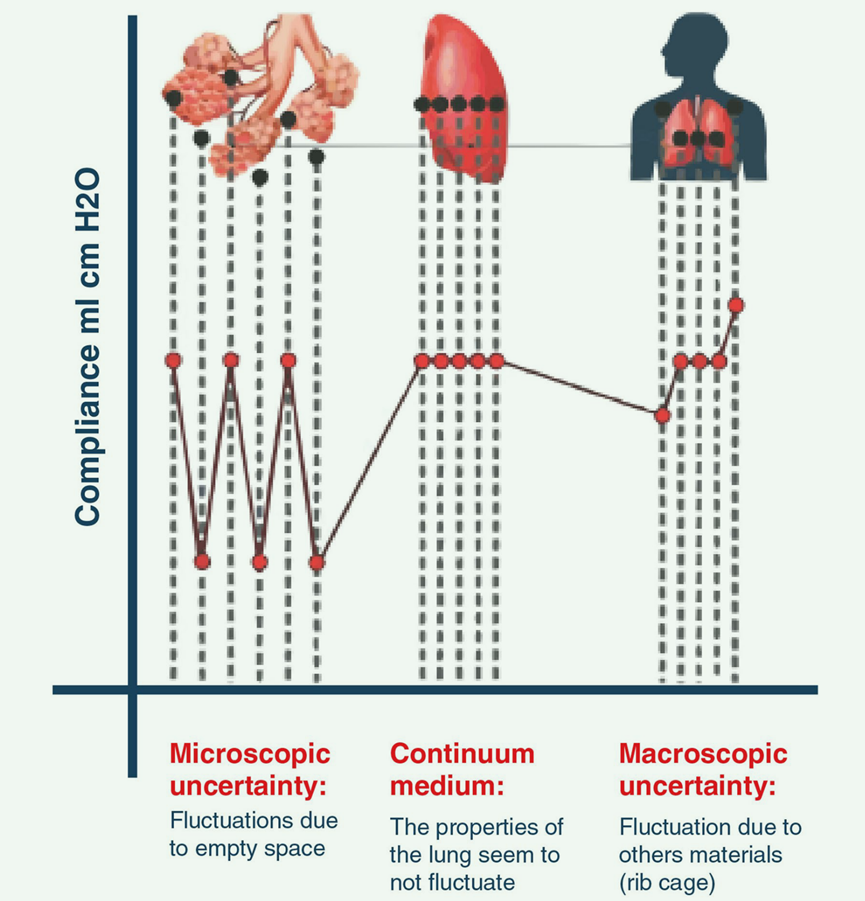
图 1 任何微观层面的监测都会为我们提供来自空腔(肺泡和胸膜之间的空间)的信息,但这些信息并不十分有用,会造成不连续性,我们称之为 "微观不确定性"。在中间尺度上,我们会发现一种连续性,因为在这一尺度上,空的部分不会被感知到,因此应该被忽略,从而提供了介质的均匀连续性(肺的特性似乎没有波动),并提供了系统的平均测量值。在宏观尺度上,也会存在不连续性,这是由其他不同材料结构(肋骨)的影响决定的,从而增加了 "宏观不确定性"。


