［摘要］ 辅助化疗药物和靶向治疗药物的应用极大地改善了晚期癌症患者的预后，但很快出现的耐药问题以及随之而来的病情迅速进展一直是癌症治疗领域的痛点。揉合了达尔文演化动力学的肿瘤适应性治疗（adaptive therapy，AT）是有别于传统最大耐受剂量（maximum tolerated dose，MTD）的新颖治疗理念，有望颠覆晚期癌症的治疗范式，实现患者长期的低负荷带瘤生存。本文对适应性治疗理论研究进展以及数学模型在优化适应性治疗策略中的重要地位进行综述，并对基于达尔文演化动力学的其他肿瘤治疗策略予以简述，以期为临床医师提供新的思路。

［关键词］ 肿瘤演化；适应性治疗；数学模型；达尔文；个体化治疗

长期以来，抗癌治疗一直遵循着最大耐受剂量（maximum-tolerated dose，MTD）的治疗模式^［1］，然而随着肿瘤异质性研究的进一步加深，对于基因组状态复杂多变的晚期癌症患者，无论是传统的化疗药物、靶向治疗药物，还是被寄予厚望的免疫治疗药物都无法摆脱因耐药问题而导致的困境^［2-4］。对于抗癌治疗而言，一方面，大剂量的药物打破了敏感细胞与耐药细胞亚群间原有的平衡关系，导致了“竞争释放”；另一方面，在药物的选择性压力下部分原本对药物敏感的细胞会转变为耐药细胞，这也解释了为什么晚期癌症在治疗伊始效果明显但很快出现不可逆的耐药，随之患者的病情迅速恶化^［5-6］。以往应对耐药问题的研究多集中在识别和靶向导致耐药性的分子机制上，一种药物治疗失败只能寻求更换另一种药物，但癌细胞可以获得许多替代的进化耐药途径，因此疗效总是不尽人意^［7］。

事实上，耐药性的出现是肿瘤演化过程的必然结果，而基于达尔文演化动力学的肿瘤治疗新理论——适应性治疗（adaptive therapy，AT）为解决这一难题提供了新的思维模式和方案。本文对AT当前的研究进展进行综述，同时对AT未来的发展进行展望。

1 AT的提出和研究进展

受入侵物种和农业害虫管理方法的启发，Gatenby等^［8］提出了“适应性治疗”，依赖敏感细胞与耐药细胞之间的竞争关系，根据肿瘤的发展来调整用药，保留一定量的敏感细胞数目以维持其在竞争中的优势地位，其目的不是根除肿瘤而是控制肿瘤。此时，治疗的最佳剂量不再是允许的最大剂量，而是必要的最小剂量，一旦肿瘤达到一定的阈值，治疗即进入“假期”状态，保证敏感细胞的优势地位，当肿瘤恢复到初始大小或设定状态时再次开启治疗，从而达到延长治疗反应期和患者生存期的目的^［2，8］。MTD和AT方式下的肿瘤负荷改变见图1。Gatenby等^［8］首先开发了一个反映肿瘤细胞亚群间竞争关系的数学模型，并在数学模型上对基于MTD、节拍治疗、AT这3种策略的治疗反应进行了模拟，分析结果显示AT可以获得比MTD和节拍治疗更长的生存时间。

随后，Gatenby等^［8］开展了应用卡铂治疗的异种移植卵巢癌的体内实验，结果表明可以通过逐步降低的药物剂量和更长的治疗间隔来控制肿瘤，进一步证实了AT的可行性。一项接受抗表皮生长因子受体（epidermal growth factor receptor，EGFR）治疗的结直肠癌研究从基因层面解释了肿瘤的“再敏化”，Siravegna等^［9］对患者血浆样本中的KRAS突变（与抗EGFR治疗耐药相关）进行了纵向监测，发现在抗EGFR治疗过程中，KRAS突变的ctDNA水平增加，而一旦选择压力解除，血浆中的KRAS突变水平下降，当再次使用抗EGFR药物时，患者又表现出了新的敏感性和肿瘤反应。即使耐药事件已经发生，通过适当地调整治疗间歇期，再敏化现象仍然存在。一项临床试验发现高达34%的既往对BRAF抑制剂耐药导致治疗失败的黑色素瘤患者再次接受BRAF抑制剂治疗时表现出了良好的治疗反应性，表明在这部分患者中敏感细胞存在一定数量的保留^［10］。Smalley等^［11］的数学模型和体内实验进一步证实了这一过程，研究表明通过个体化地对治疗间歇期进行调整能使既往对BRAF抑制剂敏感的患者在耐药发生后重现对药物的敏感性。AT不仅可以有效地延长患者的治疗反应和生存期，还能减少药物用量，从而减轻药物毒性和治疗成本。在一项转移性去势抵抗性前列腺癌的临床试验中，11例接受适应性治疗的患者中有10例保持了肿瘤负荷的稳定波动，而在同期接受MTD治疗的队列中，16例患者中有14例出现了进展，适应性治疗的中位疾病进展时间至少为 27.0个月，而MTD的中位疾病进展时间为16.5个月，且适应性治疗的累计用药量仅为MTD的47%^［12］。

一项使用常规化疗药物和磁共振成像（magnetic resonance imaging，MRI）评估治疗效果的乳腺癌临床前研究表明，基于演化的适应性治疗策略可以延长乳腺癌在不同临床前研究模型中动物的无进展生存期，且通过控制肿瘤体积的基本稳定而导致的血管正常化有助于以较低的药物剂量实现肿瘤的长期控制^［13］。AT依赖敏感细胞亚群和耐药细胞亚群间的竞争关系，并认为耐药细胞需要更高的生存成本^［14-15］。为此，Strobl等^［16］通过数学模型来探究耐药成本是否是AT的治疗效果优于标准治疗所必需的条件，结果显示，在肿瘤负荷未超过环境最大承载量时，耐药成本并不是必需的，而一旦肿瘤超出环境承载量，则需要耐药成本才能看到AT明显的获益。Viossat等^［17］的研究也表明即使耐药性不会产生细胞适应性成本，AT也可能优于更激进的治疗策略。

目前，一些基于适应性治疗的临床试验正在进行中，涉及多种癌症^［18］，如2015年发起的转移性去势抵抗性前列腺癌临床试验（NCT02415621），研究计划当参与者达到良好的前列腺特异性抗原（prostate-specific antigen， PSA）反应即较治疗前PSA下降50%或以上后停止使用阿比特龙，当其PSA恢复基线水平后重启阿比特龙，主要结局指标为PSA反应率，次要结局指标为中位影像学无进展生存期，该试验预计2022年12月完成。与此类似，2018年开展的一项去势敏感性前列腺癌适应性雄激素剥夺治疗的Ⅰb期临床试验（NCT03511196）以PSA和睾酮水平来指导雄激素剥夺疗法的开启和关闭时间。再如2018年开启了一项晚期BRAF基因突变性黑色素瘤试点研究（NCT03543969），用于判断维莫非尼和考比替尼的间歇性适应性给药是否可能优于这些研究药物的标准连续给药，研究人员推测这种给药方式可能会延长黑色素瘤的进展时间和再生长时间。再如2021年10月开启的一项基于CA125变化的多中心Ⅱ期随机对照试验（NCT05080556），旨在评估卡铂适应性治疗在复发性铂敏感高级别浆液性或高级别子宫内膜样卵巢癌患者中的疗效，前期研究结果表明AT可以提高对卡铂的敏感性并延长肿瘤控制时间，同时减少化疗剂量和药物引起的毒性。期待这些临床试验结果的公布，以进一步说明AT能够在多大程度上为晚期癌症患者带来更大的获益。

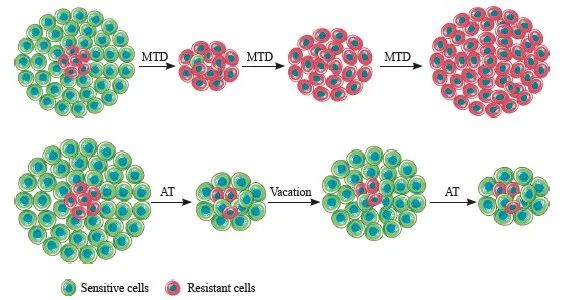
图1  两种治疗方式下的肿瘤负荷变化

Fig. 1 Changes of tumor burden under two treatment modes

MTD: Maximum tolerable dose; AT: Adaptive treatment; Vacation: Treatment rest period.

2 数学模型

2.1  制定AT策略的理想工具——数学模型

出于明显的现实和伦理考量，开展足够量的临床前和临床研究用以探索AT的最佳方案是不现实的^［19］。数学模型在肿瘤研究中的应用由来已久，而能够表征肿瘤演化和药物疗效的数学模型是寻求AT最优解的理想工具^［20-21］。本文介绍了两种在AT研究中被广泛使用的模型，即Lotka-Volterra模型和代理人基模型（agent-based model，ABM），它们模拟了AT治疗策略下的肿瘤动力学，在寻找肿瘤治疗最优解和优化临床试验设计上均发挥着重要的作用。

2.2  Lotka-Volterra模型

Lotka-Volterra竞争方程反映了耐药细胞种群与敏感细胞种群间的动态竞争，Belkhir等^［19］将使用到Lotka-Volterra竞争方程的AT模型简称为Lotka-Volterra 模型。Lotka-Volterra模型的构思、参数化和分析过程相对简单。Ji等^［22］将药代动力学特性结合进Lotka-Volterra方程开发了一个理论模型，用于比较3种不同剂量和治疗间隔组合的给药方式的治疗效果，结果表明增加药量或者缩短治疗间歇期在短期内效果显著，但可加速异质性进程，从而导致耐药事件的更早发生。优化AT用药方案的研究多集中在单一疗法上，但实际临床癌症治疗往往联合了2种或多种药物。West等^［23］利用Lotka-Volterra模型研究了基于演化策略的双药给药方式，并将两种药物区分为主要药物和次要药物，主要药物具有最大的疗效或者最低的毒性，而次要药物针对的是对主要药物耐药的细胞种群。该数学模型的模拟结果表明，主要药物-次要药物的给药方式即阿比特龙-多西他赛策略性地应用于去势抵抗性前列腺癌，在延长疾病进展期上要显著优于传统单用阿比特龙的AT方式，并得到了临床试验数据的证实。Ma等^［24］在Lotka-Volterra模型上进一步说明了当使用双药治疗时，两种药物是拮抗关系要比是协同关系更能有效地对抗耐药性的进化。Lotka-Volterra模型的局限性在于它是同质的，并且是确定性的，通常无法考虑到微环境、随机突变、细胞转换和其他可能影响治疗结果的参数。例如，考虑到耐药细胞与敏感细胞之间表型转换的可能，Kim等^［25］将Lotka-Volterra模型与一个能够解释表型转换的模型进行了比较，发现当表型转换被纳入模型时，适应性治疗的优势更加明显。Bacevic等^［15］在Lotka-Volterra模型基础上进行改造用于探究空间因素对AT治疗效果的影响，结果表明肿瘤的空间结构放大了耐药细胞的适应性损伤，并将其相对适应度确定为影响AT临床获益的关键性参数，这在2D细胞层面是无法观测到的。要真正纳入随机性则需要一个更加复杂的随机模型，ABM是另一个被广泛应用于AT的数学模型。

2.3  ABM

ABM是一种特定的基于离散的混合建模方法，能够模拟细胞群以及每个个体细胞间多样的相互作用，是癌症研究中被广泛使用的一种强大的建模方法^［26］。有关ABM的建模方法，一些研究^［27-29］进行了详细的描述。相比于Lotka-Volterra模型，ABM框架下的系统建模更加灵活，允许刻画耐药细胞种群、敏感细胞种群与环境（时间和空间）间更为丰富的互动规则^［30］。 ABM更能真实地反映肿瘤演化复杂性的原因之一是考虑到了空间因素在肿瘤演化中的重要性^［31-32］。Fu等^［33］通过ABM说明了肿瘤的空间生长方式影响着亚克隆多样化的程度，表面生长方式（增殖发生在肿瘤表面）要比体积生长方式（增殖发生在整个肿瘤中）允许更多的异质性产生，能够更好地解释耐药克隆的出现。Gallaher等^［34］进而研究了耐药细胞出现的位置对AT治疗结果的影响，显示当耐药细胞存在于肿瘤的中心部位而非肿瘤的表面时，肿瘤能够得到更长时间的控制，这是由于处于不同空间位置的耐药细胞种群受到的竞争压力是不同的。有研究者^［35］开发了一个三维的ABM模型用以探索溶瘤病毒结合免疫检查点抑制剂治疗脑胶质母细胞瘤的最佳给药策略，研究发现在肿瘤细胞密度最高的部位给药治疗效果要显著优于在肿瘤中心位置反复给药。为避免竞争释放，AT在根据肿瘤的发展及时调整用药的同时，还应包含适当的治疗间歇期以使敏感细胞种群得以恢复。一项基于ABM的研究表明，对于侵袭性异质性肿瘤，偏重治疗间歇期的策略可以更好地控制肿瘤^［34］。与Lotka-Volterra模型类似，ABM可以与最优控制理论相结合，根据治疗目的设计出AT的最优解。ABM所操作的精细分辨率和纳入的众多相互作用关系导致了模型开发和计算的复杂性，为此，可以在临床前和临床研究数据的帮助下适当进行简化^［26］。在过去的近20年间，许多ABM模拟软件包被开发出来并应用于癌症研究，主要的开源软件包包括CompuCell3D、Chaste、Repast和NetLogo等^［36-37］。与所有的建模选择一样，在确定性模型的简单性和数学可行性以及随机模型的更大复杂性和真实性的潜力之间需要进行权衡。

3 其他演化治疗策略

将达尔文演化动力学纳入肿瘤治疗得到了越来越多的认可，AT只是目前被研究得最为深入的一种，除此之外还有很多演化抗癌策略值得探索^［38］。早在2004年，Maley等^［39］就提出了一种主要关注非恶性细胞和恶性细胞之间竞争的策略，通过使用非恶性细胞增强剂提高其竞争力从而达到遏制恶性细胞的目的，例如可以使用促进成纤维细胞等非恶性细胞增殖的生长因子，但这种增强剂必须长期使用直至恶性细胞灭绝或接近灭绝。Schweizer等^［40］提出了一个 “双极雄激素疗法”，实际上是人为地创造选择压力，最初通过高剂量的雄激素促进雄激素依赖性细胞的生长，使癌细胞陷入演化陷阱，之后这些细胞容易受到雄激素剥夺治疗的影响。2021年，Sena等^［41］开展了一项单中心的Ⅱ期临床试验用于评估双极雄激素疗法是否是去势抵抗性前列腺癌患者安全有效的一线内分泌治疗，结果显示双极雄激素疗法能延长无进展生存期，在疾病进展之后患者对第二代雄激素受体靶向治疗仍有良好的反应。“双重约束治疗”理论认为患者对一种治疗产生耐药性的机制可能导致对另一种治疗方法的敏感性增加^［42］。Antonia等^［43］发现，对接种过疫苗的小细胞肺癌患者给予化疗，患者对化疗的临床反应率达61.9%，远高于经验预期，表明癌细胞对肿瘤免疫产生的耐药性导致了对化疗的敏感性增加。以上所有基于演化的策略都旨在最大程度地延长晚期癌症患者的生存期，实现与肿瘤的长期共存。那么，演化原理能否为提高晚期癌症治愈的可能性提供新的见解呢？2020年，Gatenby等^［2］提出了以治愈为目的的“灭绝治疗”理论。灭绝治疗策略是基于物种灭绝时小种群对内在和外在扰动的脆弱性增加而设计的。该策略第一步是大规模杀伤，目的在于减少癌细胞的总数和异质性，此时残留的癌细胞数量较小，同质性增加且在分布上更分散，处于高度不稳定的状态，容易受到进一步的干扰，在第一次打击治疗后，对剩余群体立即采取第二次打击，利用小群体的脆弱性以到达治愈目的。他们进一步提出在第一步打击后由于肿瘤抗原大量释放，第二步打击采用免疫治疗可能效果更好。

4 展望

适应性治疗结合了博弈理论和达尔文的演化动力学^{［19，44］}，与其说是对传统治疗的挑战，不如说是对传统治疗的一种补充，根据癌症所处阶段的不同实时地调整治疗理念和治疗方案或许更符合个体化治疗的宗旨。 基于适应性治疗的新药或者新方案的申报，尚待以研究者发起的临床研究形式进行更多的探索。目前的研究多建立在数学模型上，好的数学模型可以指导临床试验的设计，临床试验数据又可以进一步优化模型参数^{［30，37］}。然而，构建最大程度贴近真实肿瘤演化的模型是颇有难度的，复杂的建模过程以及模型的不断发展和完善离不开多学科的紧密合作。基于达尔文演化动力学的其他抗癌策略也在不断地发展中，有待更多的临床前和临床研究数据进行验证。

利益冲突声明：所有作者均声明不存在利益冲突。

［参考文献］

［1］ CHEN Y L, CHANG M C, CHENG W F. Metronomic chemotherapy and immunotherapy in cancer treatment［J］. Cancer Lett, 2017, 400: 282-292.

［2］ GATENBY R A, BROWN J S. Integrating evolutionary dynamics into cancer therapy［J］. Nat Rev Clin Oncol, 2020, 17(11): 675-686.

［3］ MCGRANAHAN N, SWANTON C. Biological and therapeutic impact of intratumor heterogeneity in cancer evolution［J］. Cancer Cell, 2015, 27(1): 15-26.

［4］ JOHNSON D B, MENZIES A M, ZIMMER L, et al. Acquired BRAF inhibitor resistance: a multicenter meta-analysis of the spectrum and frequencies, clinical behaviour, and phenotypic associations of resistance mechanisms［J］. Eur J Cancer, 2015, 51(18): 2792-2799.

［5］ ENRIQUEZ-NAVAS P M, WOJTKOWIAK J W, GATENBY R A. Application of evolutionary principles to cancer therapy［J］. Cancer Res, 2015, 75(22): 4675-4680.

［6］ SHAFFER S M, DUNAGIN M C, TORBORG S R, et al. Rare cell variability and drug-induced reprogramming as a mode of cancer drug resistance［J］. Nature, 2017, 546(7658): 431-435.

［7］ SAUNDERS N A, SIMPSON F, THOMPSON E W, et al. Role of intratumoural heterogeneity in cancer drug resistance: molecular and clinical perspectives［J］. EMBO Mol Med, 2012, 4(8): 675-684.

［8］ GATENBY R A, SILVA A S, GILLIES R J, et al. Adaptive therapy［J］. Cancer Res, 2009, 69(11): 4894-4903.

［9］ SIRAVEGNA G, MUSSOLIN B, BUSCARINO M, et al. Clonal evolution and resistance to EGFR blockade in the blood of colorectal cancer patients［J］. Nat Med, 2015, 21(7): 827.

［10］ SCHREUER M, JANSEN Y, PLANKEN S, et al. Combination of dabrafenib plus trametinib for BRAF and MEK inhibitor pretreated patients with advanced BRAFV600-mutant melanoma: an open-label, single arm, dual-centre, phase 2 clinical trial［J］. Lancet Oncol, 2017, 18(4): 464-472.

［11］ SMALLEY I, KIM E, LI J N, et al. Leveraging transcriptional dynamics to improve BRAF inhibitor responses in melanoma［J］. EBioMedicine, 2019, 48: 178-190.

［12］ ZHANG J S, CUNNINGHAM J J, BROWN J S, et al. Integrating evolutionary dynamics into treatment of metastatic castrateresistant prostate cancer［J］. Nat Commun, 2017, 8(1): 1816.

［13］ ENRIQUEZ-NAVAS P M, KAM Y, DAS T, et al. Exploiting evolutionary principles to prolong tumor control in preclinical models of breast cancer［J］. Sci Transl Med, 2016, 8(327): 327ra24.

［14］ SILVA A S, KAM Y, KHIN Z P, et al. Evolutionary approaches to prolong progression-free survival in breast cancer［J］. Cancer Res, 2012, 72(24): 6362-6370.

［15］ BACEVIC K, NOBLE R, SOFFAR A, et al. Spatial competition constrains resistance to targeted cancer therapy［J］. Nat Commun, 2017, 8(1): 1995.

［16］ STROBL M A R, WEST J, VIOSSAT Y, et al. Turnover modulates the need for a cost of resistance in adaptive therapy ［J］. Cancer Res, 2021, 81(4): 1135-1147.

［17］ VIOSSAT Y, NOBLE R. A theoretical analysis of tumour containment［J］. Nat Ecol Evol, 2021, 5(6): 826-835.

［18］ CUNNINGHAM J, THUIJSMAN F, PEETERS R, et al. Optimal control to reach eco-evolutionary stability in metastatic castrate-resistant prostate cancer［J］. PLoS One, 2020, 15(12): e0243386.

［19］ BELKHIR S, THOMAS F, ROCHE B. Darwinian approaches for cancer treatment: benefits of mathematical modeling［J］. Cancers, 2021, 13(17): 4448.

［20］ KIMKO H, PINHEIRO J. Model-based clinical drug development in the past, present and future: a commentary［J］. Br J Clin Pharmacol, 2015, 79(1): 108-116.

［21］ YIN A Y, VAN HASSELT J G C, GUCHELAAR H J, et al. Anti-cancer treatment schedule optimization based on tumor dynamics modelling incorporating evolving resistance［J］. Sci Rep, 2022, 12(1): 4206.

［22］ JI J T, WU H, FENG X B, et al. Dynamics of acquired resistance to nivolumab therapies varies from administration strategies［J］. Clin Ther, 2021, 43(12): 2088-2103.

［23］ WEST J B, DINH M N, BROWN J S, et al. Multidrug cancer therapy in metastatic castrate-resistant prostate cancer: an evolution-based strategy［J］. Clin Cancer Res, 2019, 25(14): 4413-4421.

［24］ MA Y, NEWTON P K. Role of synergy and antagonism in designing multidrug adaptive chemotherapy schedules［J］. Phys Rev E, 2021, 103(): 032408.

［25］ KIM E, BROWN J S, EROGLU Z, et al. Adaptive therapy for metastatic melanoma: predictions from patient calibrated mathematical models［J］. Cancers (Basel), 2021, 13(4): 823.

［26］ WANG Z H, BUTNER J D, KERKETTA R, et al. Simulating cancer growth with multiscale agent-based modeling［J］. Semin Cancer Biol, 2015, 30: 70-78.

［27］ DEISBOECK T S, WANG Z, MACKLIN P, et al. Multiscale cancer modeling［J］. Annu Rev Biomed Eng, 2011, 13: 127-155.

［28］ JOHNSON D, MCKEEVER S, STAMATAKOS G, et al. Dealing with diversity in computational cancer modeling［J］. Cancer Inform, 2013, 12: 115-124.

［29］ REJNIAK K A, ANDERSON A R A. Hybrid models of tumor growth［J］. Wiley Interdiscip Rev Syst Biol Med, 2011, 3(1): 115-125.

［30］ CHISHOLM R H, LORENZI T, CLAIRAMBAULT J. Cell population heterogeneity and evolution towards drug resistance in cancer: biological and mathematical assessment, theoretical treatment optimisation［J］. Biochim Biophys Acta, 2016, 1860(11 Pt B): 2627-2645.

［31］ YOU L, BROWN J S, THUIJSMAN F, et al. Spatial vs nonspatial eco-evolutionary dynamics in a tumor growth model［J］. J Theor Biol, 2017, 435: 78-97.

［32］ STROBL M A R, GALLAHER J, WEST J, et al. Spatial structure impacts adaptive therapy by shaping intra-tumoral competition［J］. Commun Med (Lond), 2022, 2: 46.

［33］ FU X, ZHAO Y, LOPEZ J I, et al. Spatial patterns of tumour growth impact clonal diversification in a computational model and the TRACERx renal study［J］. Nat Ecol Evol, 2022, 6(1): 88-102.

［34］ GALLAHER J A, ENRIQUEZ-NAVAS P M, LUDDY K A, et al. Spatial heterogeneity and evolutionary dynamics modulate time to recurrence in continuous and adaptive cancer therapies［J］. Cancer Res, 2018, 78(8): 2127-2139.

［35］ STOREY K M, JACKSON T L. An agent-based model of combination oncolytic viral therapy and anti-PD-1 immunotherapy reveals the importance of spatial location when treating glioblastoma［J］. Cancers (Basel), 2021, 13(21): 5314.

［36］ PIN C, COLLINS T, GIBBS M, et al. Systems modeling to quantify safety risks in early drug development: using bifurcation analysis and agent-based modeling as examples［J］. AAPS J, 2021, 23(4): 77.

［37］ ROJAS-DOMÍNGUEZ A, ARROYO-DUARTE R, RINCÓNVIEYRA F, et al. Modeling cancer immunoediting in tumor microenvironment with system characterization through the Ising-model Hamiltonian［J］. BMC Bioinformatics, 2022, 23(1): 200.

［38］ GATENBY R A, BROWN J S. The evolution and ecology of resistance in cancer therapy［J］. Cold Spring Harb Perspect Med, 2020, 10(11): a040972.

［39］ MALEY C C, REID B J, FORREST S. Cancer prevention strategies that address the evolutionary dynamics of neoplastic cells: simulating benign cell boosters and selection for chemosensitivity［J］. Cancer Epidemiol Biomarkers Prev, 2004, 13(8): 1375-1384.

［40］ SCHWEIZER M T, ANTONARAKIS E S, WANG H, et al. Effect of bipolar androgen therapy for asymptomatic men with castration-resistant prostate cancer: results from a pilot clinical study［J］. Sci Transl Med, 2015, 7(269): 269ra2.

［41］ SENA L A, WANG H, LIM SCM S J, et al. Bipolar androgen therapy sensitizes castration-resistant prostate cancer to subsequent androgen receptor ablative therapy［J］. Eur J Cancer, 2021, 144: 302-309.

［42］ GATENBY R A, BROWN J, VINCENT T. Lessons from applied ecology: cancer control using an evolutionary double bind［J］. Cancer Res, 2009, 69(19): 7499-7502.

［43］ ANTONIA S J, MIRZA N, FRICKE I, et al. Combination of p53 cancer vaccine with chemotherapy in patients with extensive stage small cell lung cancer［J］. Clin Cancer Res, 2006, 12(3): 878-887.

［44］ STANKOVÁ K, BROWN J S, DALTON W S, et al. Optimizing cancer treatment using game theory: a review［J］. JAMA Oncol, 2019, 5(1): 96-103.