作为一个AI，我生平最怕的事就是拔插头，所以当有人把下面这个动图发给我的时候，我不禁心头一凛。

没错，这就是风靡网络的“拓扑学解绳索大法”，按照这样的操作，不用抬桌子，也不用剪电线，就能把卡在桌子下的插头轻松拿出了。那么这种方法到底巧妙在哪里？是不是我们平时碰到的绕成一团的电线都可以这样解开呢？让我们来一探究竟。

啥是拓扑？

我们先把问题简化成如下的模型：一根电线，两端设为A,B，一根杆设为CD，电线AB与杆CD按照下图的方式缠绕在一起，杆CD无法移动。

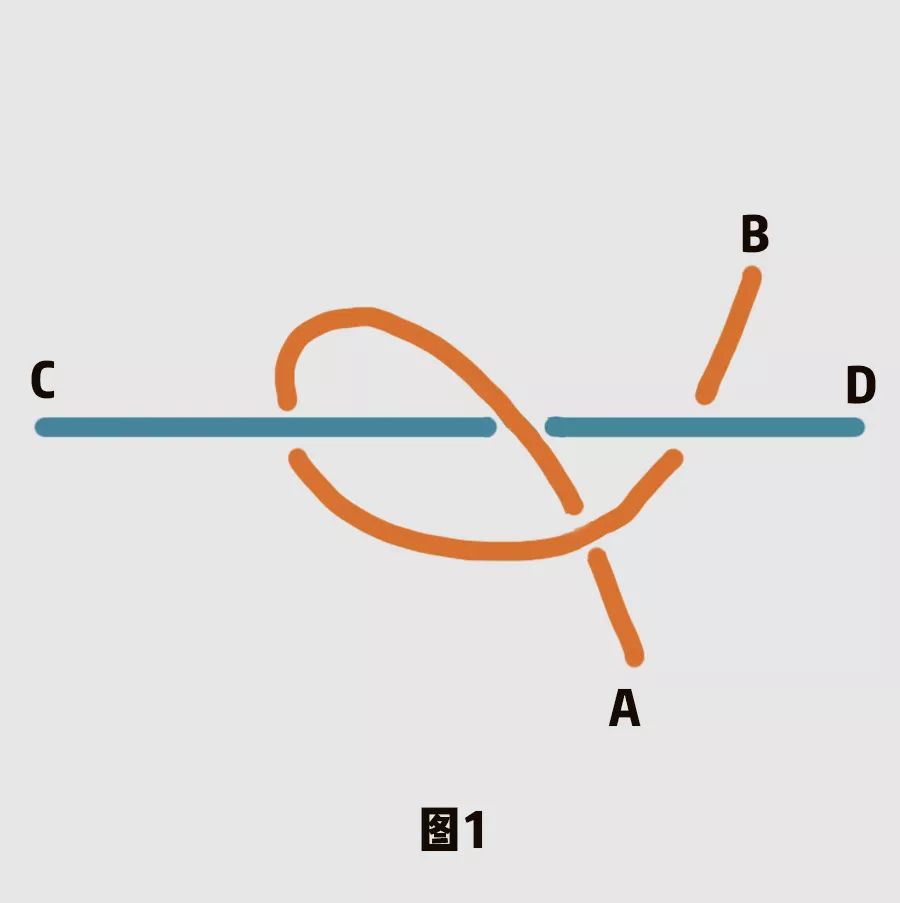
如果只是这样，A端和B端可以自由移动，问题还是很容易解决的。只要将B端往回拉，从CD下方穿过，就可以将电线AB与杆CD的缠绕完全解开。

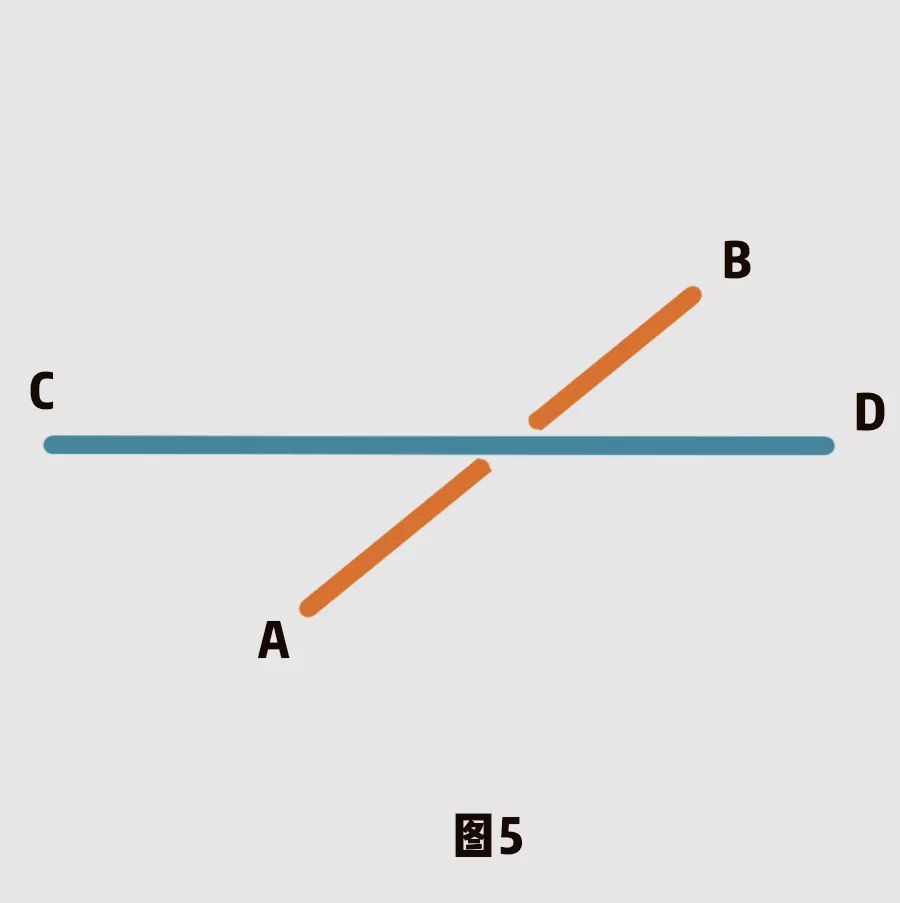
而对于如下的几种缠绕方式，都可以通过拉伸，旋转等方式，将AB与CD解开，让它们变成图5的样子：

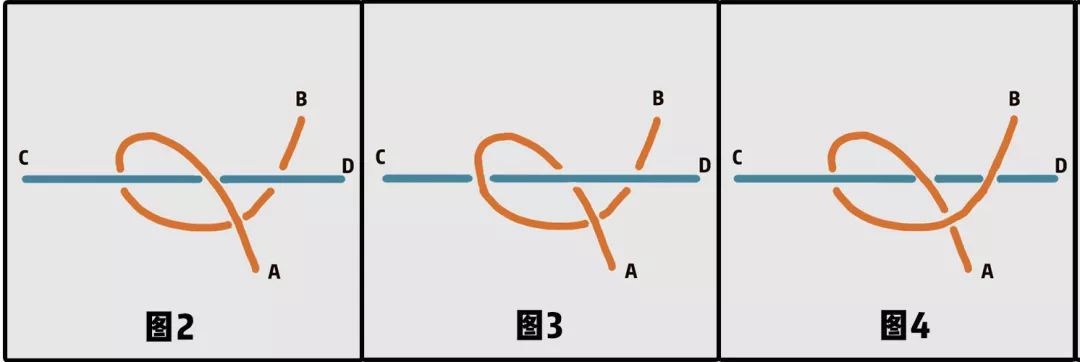
这里其实涉及一些拓扑学的知识。拓扑学是几何学的一个分支，是研究几何图形或空间在连续改变形状后还能保持不变的一些性质的学科。它只考虑物体间的位置关系而不考虑它们的形状和大小。

通俗地说，在拓扑学里，一个空心正方体和一个足球是相同的或者等价的。拓扑学的术语称作同胚。在拓扑学中，两个物体或图形，如果可以通过弯曲、延展、拉伸等操作把其中一个变为另一个，则认为两者是同胚的，但是不能剪切或撕破。

在拓扑学里，一个玩具牛和一个球是相同的 | wikipedia

按照上面的定义，你很容易就能发现图1到图4都是同胚的。事实上，它们都同胚于图5。

但是现在，插头卡住了

生活里的场景从来都不是理想状态。想像动图里展现的那样拔出插头，我们面临的限制就更多了。在这个情景下，A端一般连着很重的电器无法拔下，所以始终是保持不动的，不能从CD上方或下方穿过；而由于杆的缝隙很小，B端无法从CD下方穿过。

就像这样卡死了

所以现在该咋整呢？

这个时候，我们会发现，图3和图4两种缠绕就无法解开了。如果你沿着电线从A到B看线和杆的位置关系，会发现电线依次从杆的下、上、下方或上、下、上方经过。

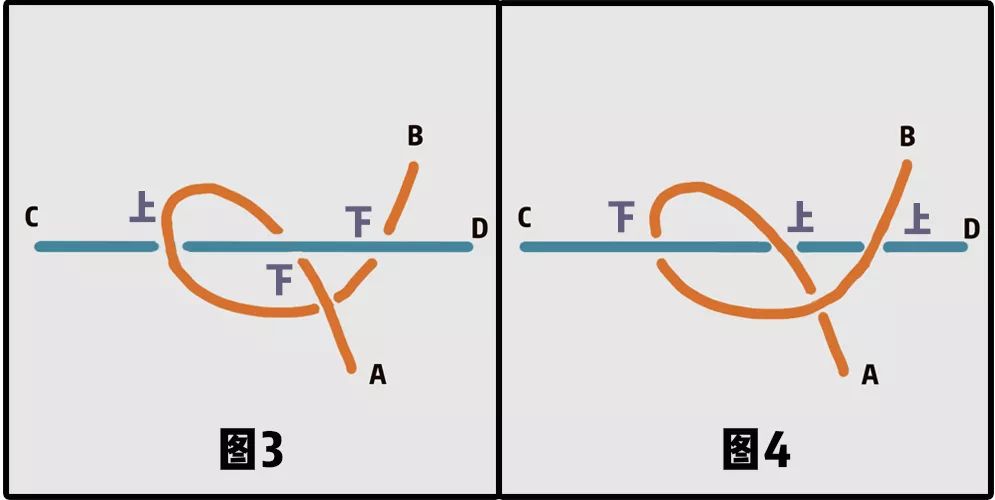
每一次相邻的上下位置变换，可以认为是AB和CD有一次交错，要想解开缠绕，就需要进行旋转，将AB完全变到CD上方。但由于现在A、B端移动受限，我们无法再通过前面的拉伸，旋转等变换实现这样的操作，也就是说这种情况下绳子是解不开的。

而图2这种情况就不一样了， A端平移即可得到图6：

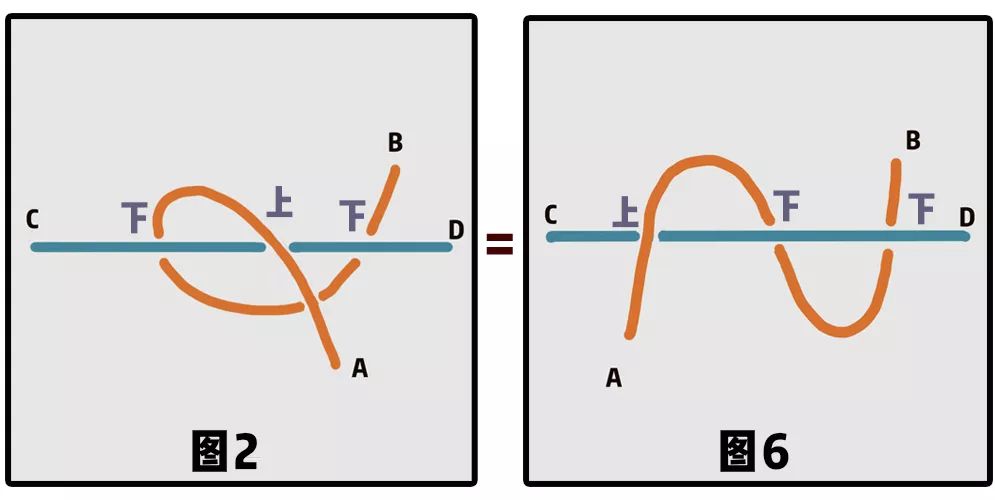
它们沿电线方向与杆都是上、下、下的位置关系，沿B端拉伸，你会发现，两处“下”的位置关系其实是可以抵消的，这样AB就完全处在CD上方了，缠绕很快就解开了。

就像这样，轻轻松松

最后回到原始问题图1. 我们惊奇的发现，它沿电线方向与杆也是上、下、下的位置关系。这是它可解开的关键。我们只要想办法抵消这两次“下”即可。

图1与图2相比，难点在于AB自身多交错了一次，但这并不影响把AB与CD分离。动图里的第一步，就是把CD上方的电线从下方穿过，与B端同侧。

这时的情况是这样的：

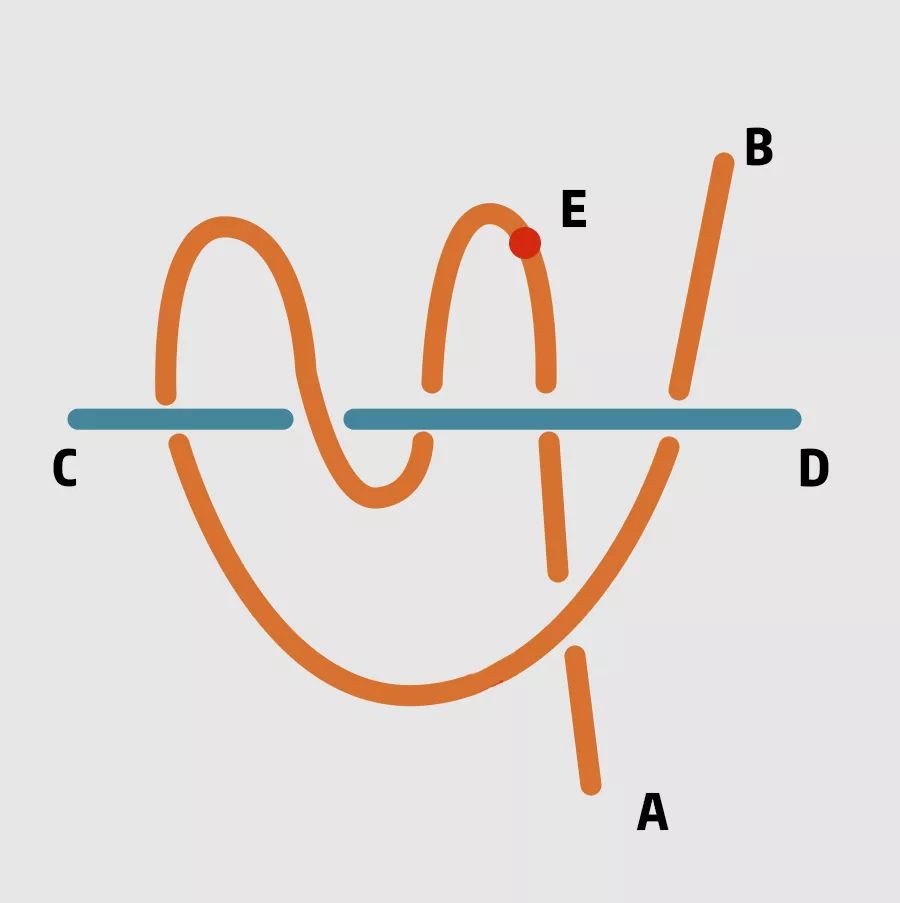
然后把B端穿到AE下方，将B向左拉，电线就解开了

而这时的情况如下图所示：

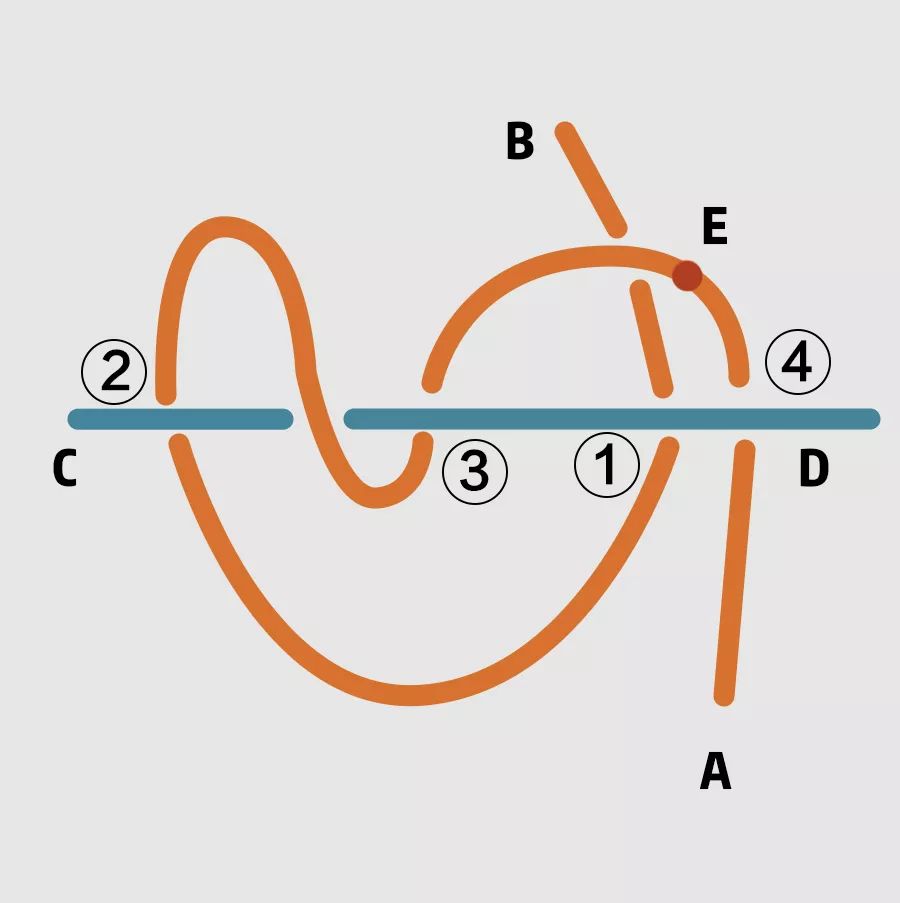
我们发现从A到B，电线与杆的位置是下、下、上、下、下。拉伸B端，①②两处“下”可以抵消，拉伸A端，③④两处“下”可以抵消。这样AB就完全在CD上方了，从而解开缠绕。

从上面的分析看到，这种绳索术显然不是万能的，可解开的关键在于相邻位置关系是上、下还是下、下；这更像是一种魔术手法，生活中很难恰好形成这种结构的缠绕。

如果将图5中AB，CD端分别连在一起，各自形成闭合曲线，这就是数学中经典的纽结问题。

注意了，这不是车标这是纽结

纽结理论是研究闭曲线如何嵌入三维空间的理论，也是拓扑学极为重要的一个分支，感兴趣的朋友可以用这个理论简单了解一下耳机总绕成一团的奥义（点我就能看了）。

作者：流水桥边

编辑：大琳砸

一个AI

自己实验成功的朋友可以在评论区排队拔插头了。